Computation Physics
Python code
Information & Computation Physics
Information Physics
Mandelbrot
2021-2 Information Physics: Mandelbrot Plot
MAX_ITER = 10000
def mandelbrot(c):
z = 0
n = 0
while abs(z) <= 2 and n < MAX_ITER:
z = z*z + c
n += 1
return n
[ mandelbrot.py ]
Computation Physics
Solution of Nonlinear Equation
- The Relaxation Method(RM)
However, there are some solutions to some equations that you cannot
find by this mehod no matter what starting value you choose
[
RM.py
]
- Binary Search-Bisection Method
[ bisection.py ]
- Newton-Raphson Method(NRM)
[ NRM.py ]
- Secant Method(SM)
generalized version of Newton-Raphson method
[
SM.py
]
Derivatives
- Taylor Expansion
Two Point
[
taylor_expansion2.py
]
Three Point
[
taylor_expansion3.py
]
Second Order
[
taylor_sec_order.py
]
Integrals
- Rectangular Method
[ rec_method.py ]
- Trapezoidal Method
[ trape_method.py ]
- Simpson’s Rule
Simpson’s 1/3 Rule
[
simp_13.py
]
Simpson’s 3/8 Rule
[
simp_38.py
]
- Monte Carlo Integration
[ MC.py ]
ex) Buffon’s Needle with Monte Carlo Method
[
buffon_niddle.py
]
ODE; Ordinary Differential Equation
First Order Differential Equations with one variable
- Euler’s Method
[ EM.py ]
- Picard Method ( Predictor-Corrector Method; PCM )
[ PCM.py ]
- Runge-Kutta Method
2nd-order Runge-Kutta is the same with the Predictor-Corrector(or Modified Euler Method)
second order
[
RM2.py
]
fourth order
[
RM4.py
]
More than one variable
[
RM_variables.py
]
Second Order Differential Equations
- Runge-Kutta Method( Second order )
[ RM2order.py ]
- Revisit Newton’s Equation of motion
Newton’s method + 4th Runge-Kutta method
example about “Van del Pol Oscillator”
[
RN.py
]
Boundary Value Problems
- Shooting Method
[ shooting.py ]
- Secant Method
[ secant.py ]
- Relaxation Method
[ relaxation.py ]
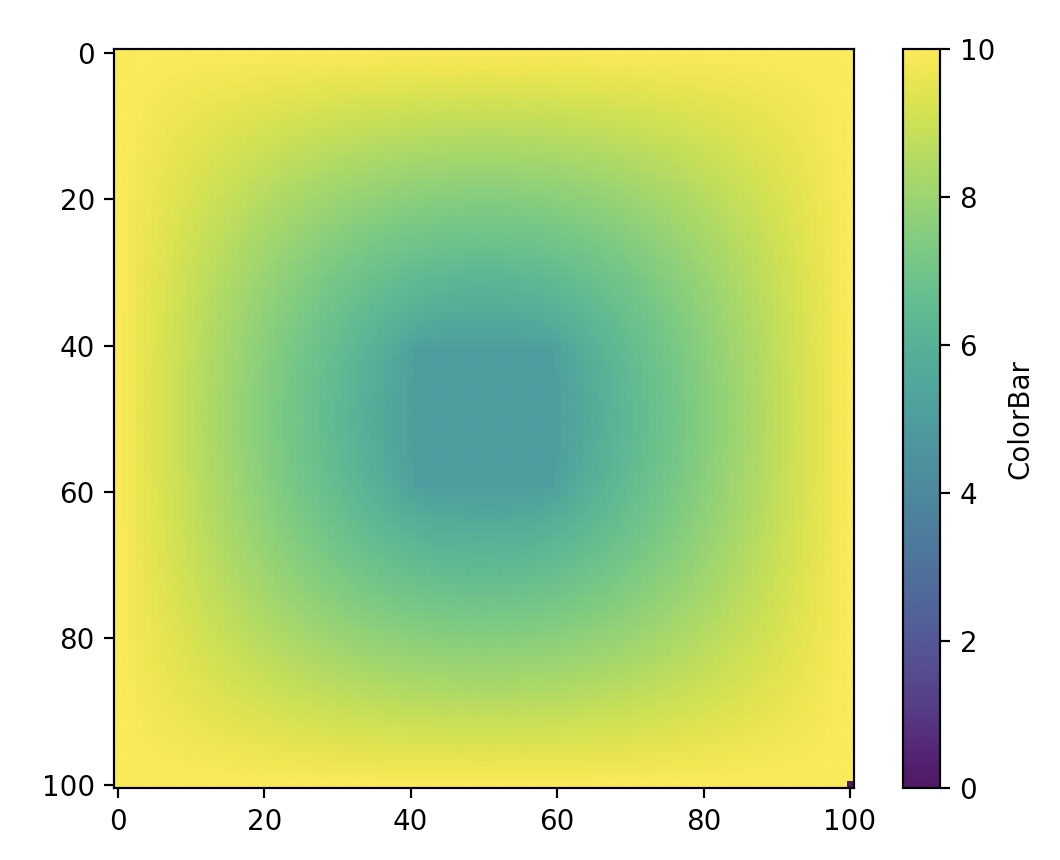
PDE; Partial Differential Equation
Laplacian Operator
Relaxation Method in 2-Dimensional Space
[
laplace.py
]
Poisson Equation
[ poisson.py ]
Solution of Linear Equations
Gauss-Jordan Elimination
rules of Gauss-Jordan Elimination
[
gaussJordan.py
]
Partial Pivoting
[
partial_Pivoting.py
]
LU Decomposition with partial pivoting
[ LU.py ]
Inverse Matrix ( with LU )
[ inverse.py ]
Tridiagonal Matrices
example about “Vibration in a One-Dimensional System”
[
tridiagonal.py
]
Eigenvectors & Eigenvalues
Get Eigenvectors and Eigenvalues by QR decomposition(Gram-Schmidt Orthogonalization)
[
eigen.py
]
Fitting: LSE fit and Extrapolation
Maximum Liklihood
[ MaxLik.py ]
Gradient Descent
Interpolation
Lagrange Interpolation
[Examples]
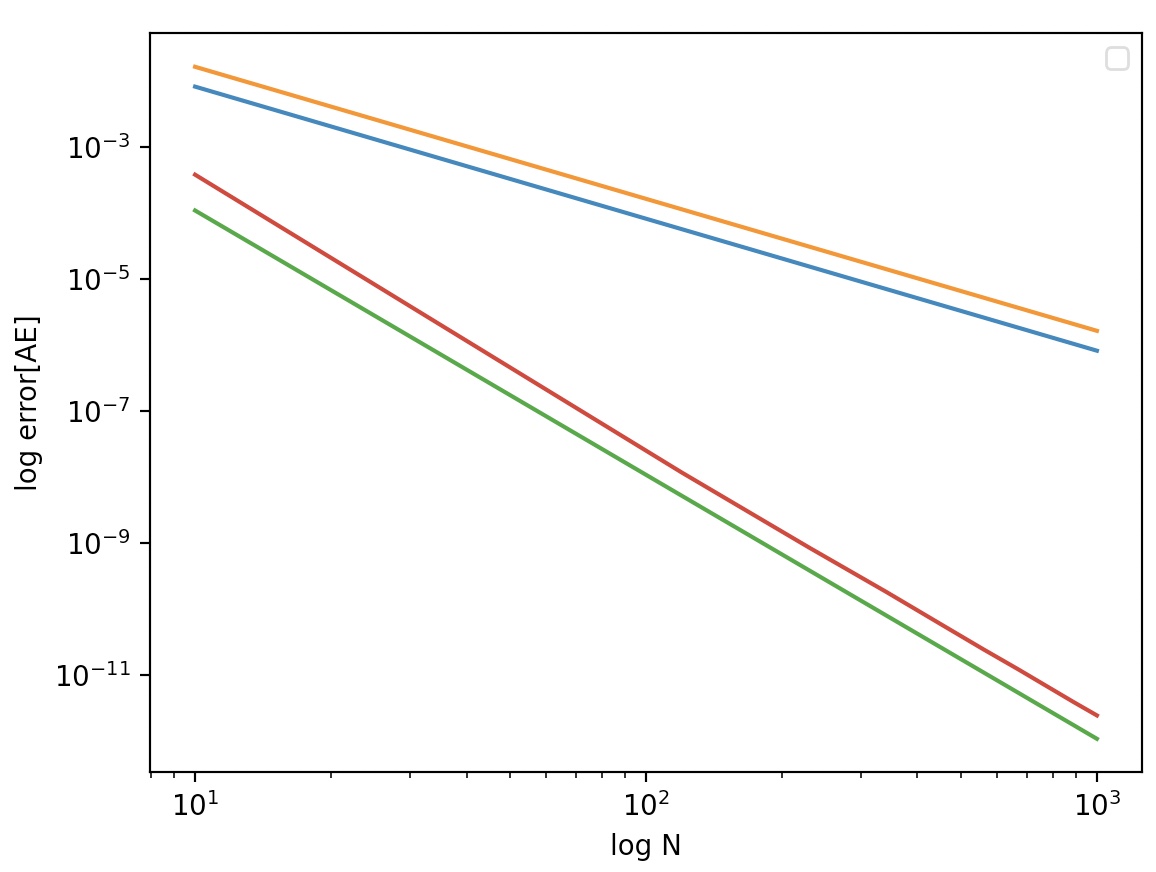
Integral method error
compare error between
Rectangular method, Trapezoidal method, Simpson 1/3 Rule, Simpson 3/8 Rule
[
error_dis.py
]
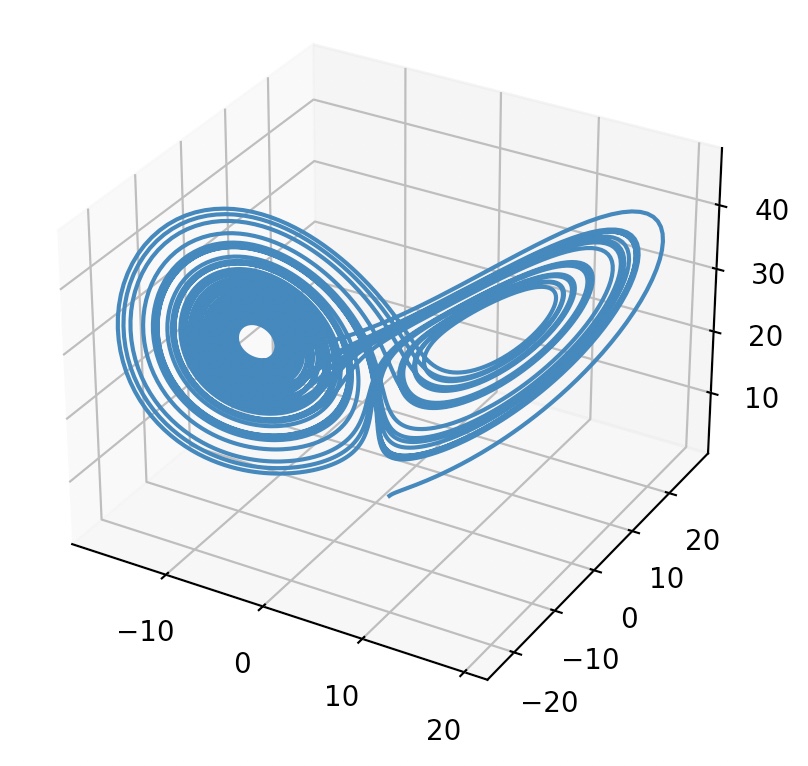
Lorenz Equation & Lotka-Volterra equation
[
lorenz.py
]
Damped Harmonic Motion ( with 4th_RKM )
Driven Pendulum
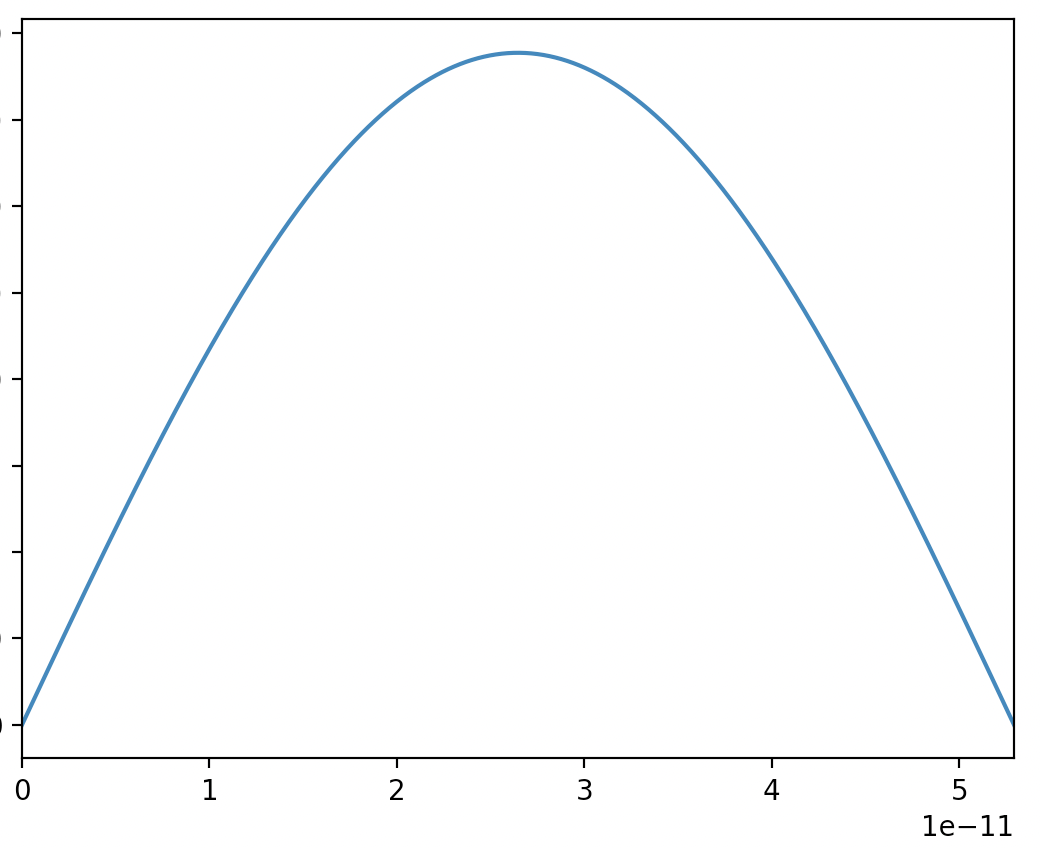
Solve Schrodinger Equation
Infinite Potential Well Ground State
[
sd_infinite.py
]
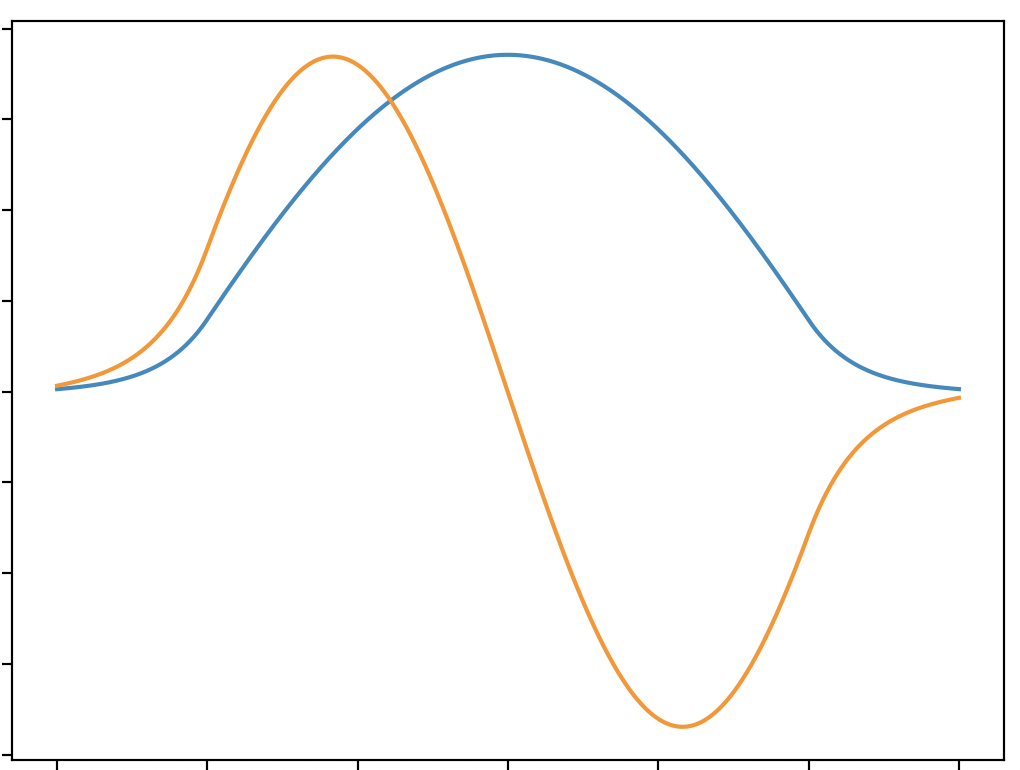
Finite Potential Well First & Second state
[
sd_finite.py
]
Electric Potential
solve electric potential PDE with relaxation method
[
elec_potential.py
]