t.test(x, y=NULL, alternative=c('two.sided', 'less', 'greater'), mu=0,
paired=FALSE, var.equal=FALSE, conf.level=0.95)
일 표본 t-검정(one sample t-test)
하나의 모집단 평균(n) 값을 특정값과 비교한느 경우 사용
일 표본 단측 t-검점
> weights<-runif(10, min=49, max=52)
> t.test(weights, mu=50, alternative='greater’) # 반대 방향은 ‘less’ 사용
One Sample t-test
data: weights
t = 2.6957, df = 9, p-value = 0.01228
# 대립 가설: 지우개의 평균 중량은 50g 보다 크다.
alternative hypothesis: true mean is greater than 50
95 percent confidence interval:
50.24982 Inf
sample estimates:
mean of x
50.7807
검정 결과 검정 통계량 t=2.6957 이며, 자유도는 표본의 개수보다 1 적은 df=9 이다.
p-value가 유의 수준 0.05 보다 작으므로 귀무가설을 기각 가능
일 표본 양측 t-검정
> weights<-runif(100, min=40, 100)
> t.test(weights, mu=70, alternative='two.sided')
One Sample t-test
data: weights
t = 0.10914, df = 99, p-value = 0.9133
alternative hypothesis: true mean is not equal to 70
95 percent confidence interval:
66.65786 73.73119
sample estimates:
mean of x
70.19452
검정 통계량 t=0.10914 이며, 자유도는 n-1 df=99이다.
p-value가 유의수준 0.05보다 작지 않으므로 귀무가설을 기각할 수 없다.
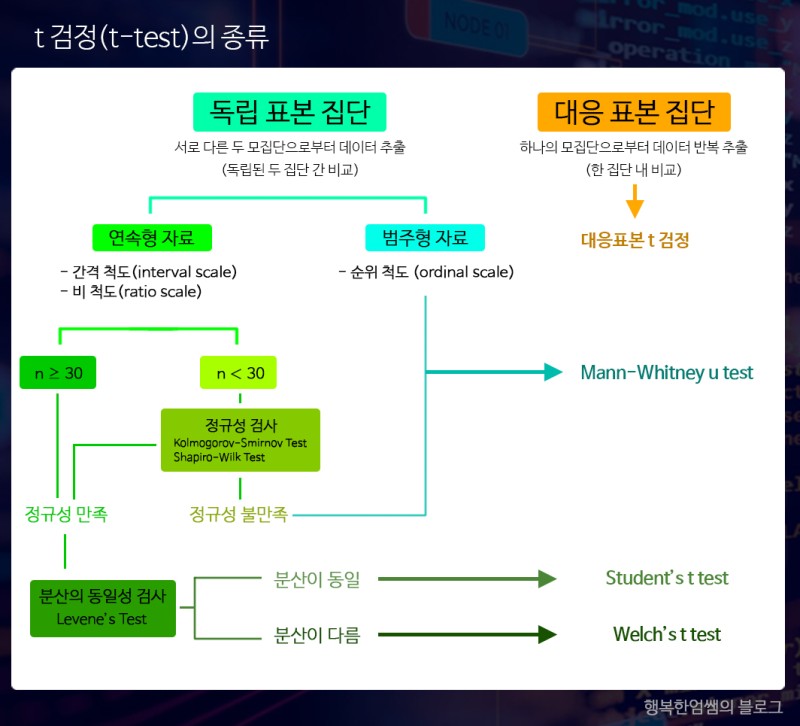
이(독립) 표본 t-검정(independent sample t-test)
서로 독립적인 집단에 대하여 모수(모평균)의 값이 같은 값을 갖는지 통계적으로 검정
모집단 분산이 같음을 의미하는 등분산성을 만족해야 한다.
(t-검정을 수행하기 전에 등분산 검정(F 검정)을 먼저 수행해야 한다.)
이 표본 단측 t-검정
> salaryA<-runif(100, min=250, max=380)
> salaryB<-runif(100, min=200, max=400)
> t.test(salaryA, salaryB, alternative='less')
Welch Two Sample t-test
data: salaryA and salaryB
t = 2.8725, df = 167.26, p-value = 0.9977
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf 31.66742
sample estimates:
mean of x mean of y
318.3956 298.2997
검정 통계량 t=2.8725이고, 자유도는 df=167.26이다.
p-valuesms 0.9977로 유의수준 0.05보다 크다(귀무가설을 기각할 수 없다.)
salaryA가 salaryB보다 같거나 많다고 말할 수 있다.
이 표본 양측 t-검정
> speedK<-runif(100, min=30, max=40)
> speedL<-runif(100, min=25, max=35)
> t.test(speedK, speedL, alternative='two.sided')
Welch Two Sample t-test
data: speedK and speedL
t = 14.151, df = 197.96, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
4.605020 6.096261
sample estimates:
mean of x mean of y
35.22861 29.87797
p-value가 유의수준 0.05보다 작기 때문에 귀무가설을 기각할 수 있다.
대응 표본 t-검정(paired t-test)
동일한 대사에 대해 두 개의 관측치가 있는 경우 이를 비교하여 차이가 있는지 검정
가정
1. 관측치가 정규분포를 따라야 한다.
2. 표본 집단(condition)이 두 개여야 한다.
3. 독립변수가 하나여야 한다.(독립변수가 많아지면 Factorial ANOVA를 사용)
4. 두 집단이 독립적이지 않다.
> before<-runif(100, min=60, max=80)
> after<-before+rnorm(10, mean=-3, sd=2)
> t.test(before, after, alternative='greater', paired=TRUE)
Paired t-test
data: before and after
t = 10.625, df = 99, p-value < 2.2e-16
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
1.597857 Inf
sample estimates:
mean of the differences
1.893806
p-value가 유의수준(0.05)보다 작기 때문에 귀무 가설을 기각할 수 있다.
(두 집단의 평균의 차이는 0보다 크다. 체중 감량 효과가 있다.)