Derivatives
- Taylor Expansion
- First-Order Derivative
- Second-Order Derivative
Fundamental Methods for Evaluating Integrals
- Rectangular Method
- Trapezoidal Method
- Simpson’s Rule
- Mote Carlo Method
- Multidimensional Integral
- Improper Integral
- Taylor Expansion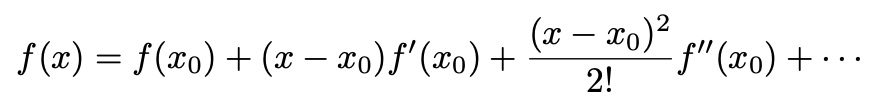
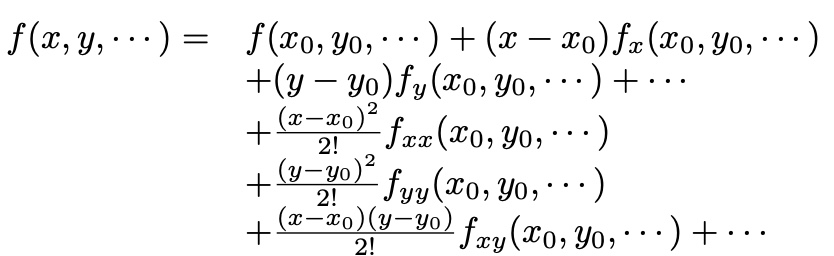

 error=O(h); h=x-x0
error=O(h); h=x-x0
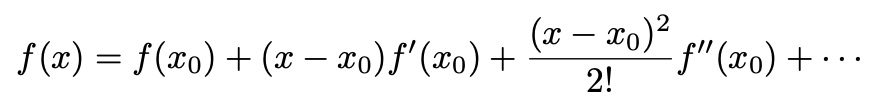
single variable function f(x)
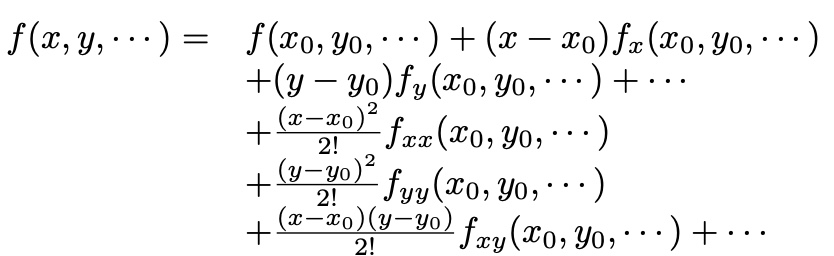
multivariable function f(x, y, …)
Two-Point formula(Taylor expansion 2항까지만 사용)

forward difference || backward difference
 error=O(h); h=x-x0
error=O(h); h=x-x0# dsin(x)/dx
import math as m
import numpy as np
import matplotlib.pyplot as plt
def sin(x):
return np.sin(x)
# two point formula
def df_dx_forward(f, x, h):
return (f(x+h)-f(x))/h
def df_dx_backward(f, x, h):
return (f(x)-f(x-h))/h
if __name__=="__main__":
x=np.linspace(0, 2*np.pi, 1000)
dydx_f=np.zeros(len(x))
dydx_b=np.zeros(len(x))
h=1e-6
i=0
for xx in x:
dydx_f[i]=df_dx_forward(sin, xx, h)
dydx_b[i]=df_dx_backward(sin, xx, h)
i+=1
plt.plot(x, dydx_f, 'b-.')
plt.plot(x, dydx_b, 'r--')
plt.show()
Three-Point formula(Two-Point formula 보다 오차가 줄어듬) Taylor Series expansion
Taylor Series expansion
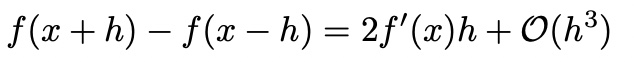
 error O(h^2)
error O(h^2)
 Taylor Series expansion
Taylor Series expansionthen,
 error O(h^2)
error O(h^2)(Two-Point formula 오차 O(h)에서 O(h^2)로 1보다 작은 h에 대하여 오차 감소)
수학적으로 two-point formula foward와 backward의 평균
# dsin(x)/dx
import math as m
import numpy as np
import matplotlib.pyplot as plt
def sin(x):
return np.sin(x)
def df_dx_tp(f, x, h): # three point formula
return (f(x+h)-f(x-h))/(2*h)
if __name__=="__main__":
x=np.linspace(0, 2*np.pi, 1000)
dydx_t=np.zeros_like(x, float)
h=1e-6
i=0
for xx in x:
dydx_t[i]=df_dx_tp(sin, xx, h)
i+=1
plt.plot(x, dydx_b, 'r--')
plt.show()
- Second Order Derivative


Taylor Series for f(x)
from

then,

import numpy as np
import matplotlib.pyplot as plt
def sin(x):
return np.sin(x)
def d2f_dx2(f, x, h):
result=f(x+h)+f(x-h)-2*f(x)
result/=h**2
return result
if __name__=='__main__':
x=np.linspace(-2*np.pi, 2*np.pi, 100)
ddf=np.zeros_like(x, float)
for i in range(len(x)):
ddf[i]=d2f_dx2(sin, x[i], 1e-6)
anal=-np.sin(x)
plt.plot(x, ddf, 'ro', ms=4)
plt.plot(x, anal, 'k-', lw=3)
plt.show()