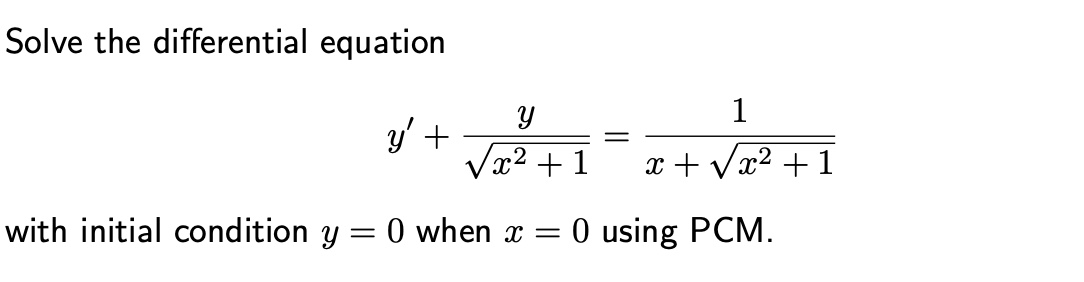
# PCM HW12
# dy/dx=1/(x+sqrt(x^2+1))-y/sqrt(x^2+1)
import numpy as np
import matplotlib.pyplot as plt
def f(y, x): # dy/dx=f(x, y)
return 1/(x+np.sqrt(x**2+1))-y/np.sqrt(x**2+1)
def PCM(f, x, t):
h=t[1]-t[0]
for i in range(len(t)-1):
xx=x[i]+f(x[i], t[i])*h
x[i+1]=x[i]+h*(f(x[i], t[i])+f(xx, t[i+1]))/2
return x
if __name__=="__main__":
x_i=0; y_i=0
x_f=1
x=np.linspace(x_i, x_f, 1000)
y=np.zeros_like(x, float)
y[0]=y_i
y=PCM(f, y, x)
plt.plot(x, y)
plt.show()
simple
def dydx(x, y):
return 1/(x+np.sqrt(x**2+1))-y/np.sqrt(x**2+1)
x=np.linspace(0, 1, 1000)
y=np.zeros_like(x)
y[0]=0
h=x[1]-x[0]
for i in range(len(x)-1):
#y[i+1]=y[i]+dydx(x[i], y[i])*h
yy=y[i]+dydx(x[i], y[i])*h
y[i+1]=y[i]+(dydx(x[i], y[i])+dydx(x[i+1], yy))*h/2