Numerical Integration(symbolic calculation 아님)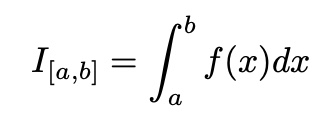
Not all integrations are carried out analytically
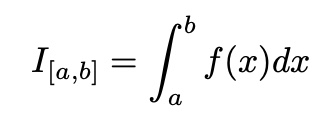
- Rectangular Method
Divied the interval [a, b] into N subintervals: N*h=b-a
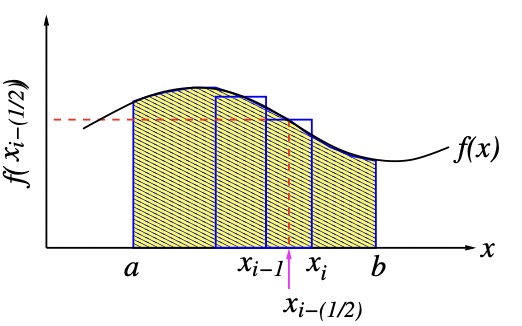
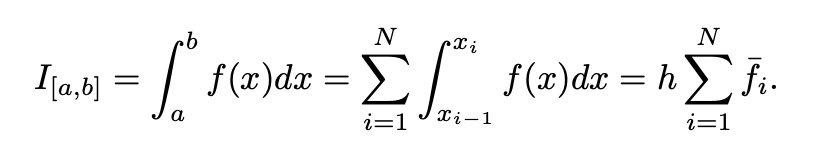
from Taylor expansion at x=i-1/2(Rectangular Method-Error Estimation)
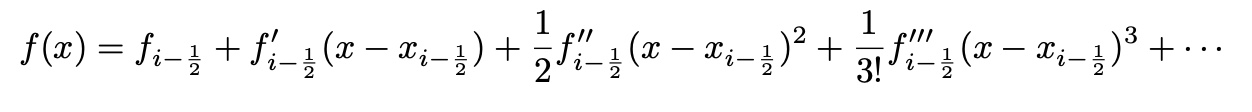
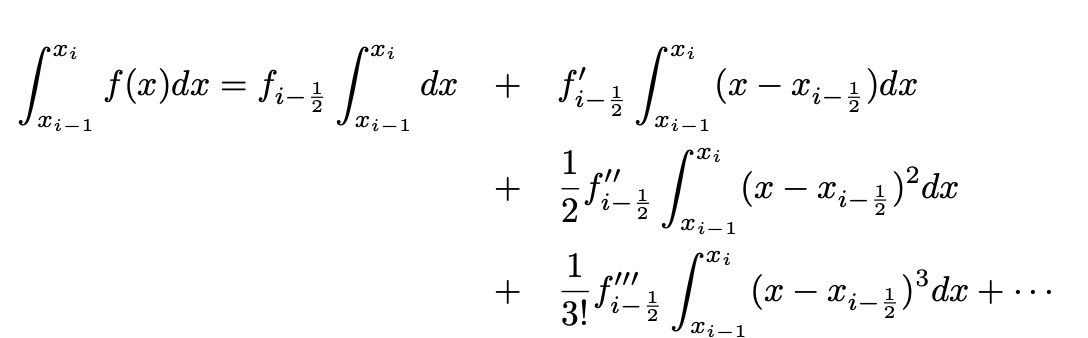

import numpy as np
def f(x):
return x**4-2*x+1
def integrate(f, x0, x1, N):
s0=0.
x=x0
h=(x1-x0)/N
for i in range(0, N):
s0+=f(x+h/2.)*h
x+=h
return s0
x=np.linspace(0, 2, 100)
h=x[1]-x[0]
integ_res=0.
for i in range(len(x)-1):
integ_res+=f((x[i]+x[i+1])/2)*h
print(integ_res)
# sum=integrate(f, 0, 2, 100)
# print(sum)
sin 적분
import numpy as np
import matplotlib.pyplot as plt
def sin(x):
return np.sin(x)
def integrate(f, x0, x1, N=100):
s0=0.
h=(x1-x0)/N
x=x0
for i in range(0, N):
# *h 연산은 루프밖으로 빼서 처리하는 것이 좋음
s0+=f(x+h/2.)*h
x+=h
return s0
if __name__=='__main__':
N=100
sum=integrate(sin, 0, np.pi, N)
print("integral: ", sum, sep='')
- Trapezoidal Method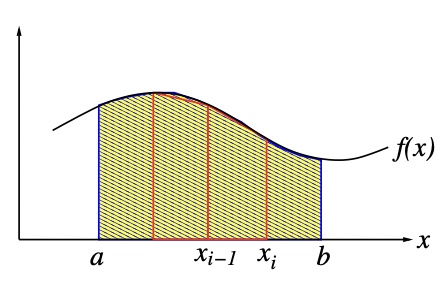
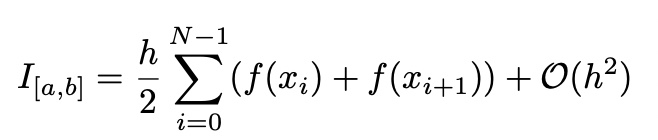

Simpply replace the recangles by trapezoids
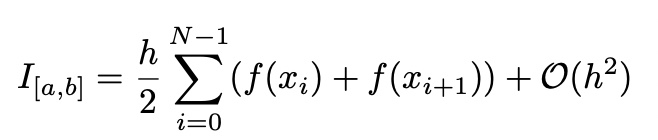
h에 대한 오차는 Rectangular Method와 Trapezoidal Method가 동일
(상황에 따라서 더 정확한 방법이 다르다)
import numpy as np
def f(x):
return x**4-2*x+1
def integrate_tz(f, x0, x1, N=100):
s0=0.
h=(x1-x0)/N
x=x0
for i in range(0, N):
# *h/2 연산은 루프 밖으로 빼서 처리하는 것이 좋음
s0+=(f(x)+f(x+h))*h/2
x+=h
return s0
if __name__=='__main__':
N=100
sum=integrate_tz(f, 0, 2, N)
print("integral: ", sum, sep='')
Simpson’s Rule


to improve the accuracy
기존에 retangular Method와 Trapezoidal Method가 오차가 O(h^2)라면,
Simplson’s Rule은 O(h^5)의 오차를 가짐
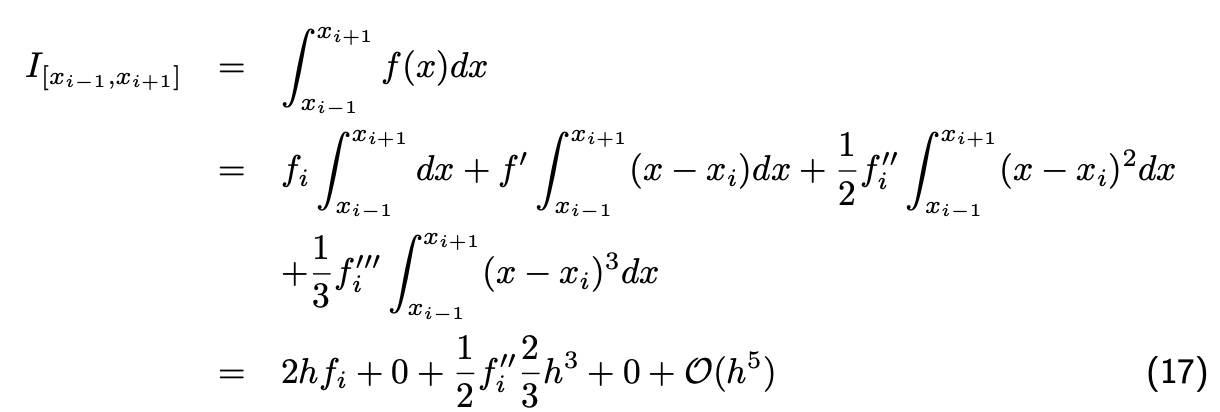
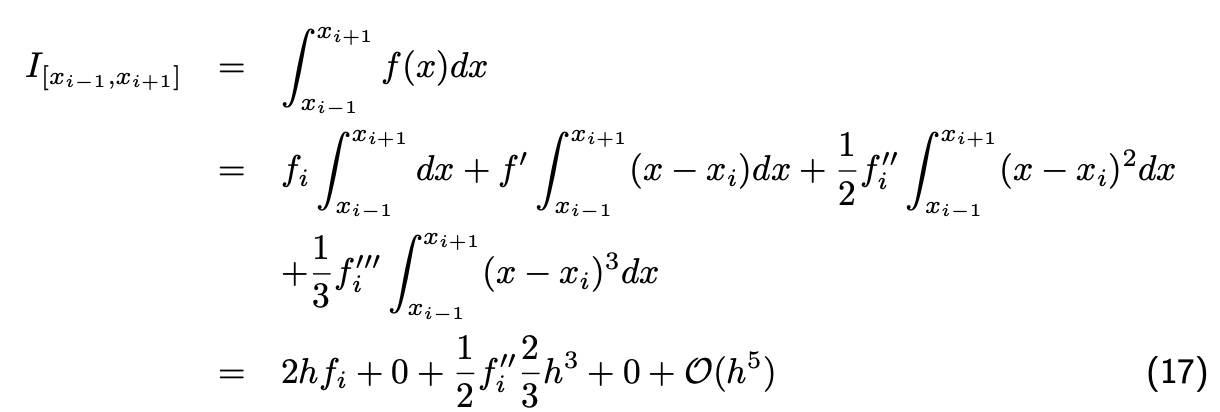
from


then,

import numpy as np
def f(x):
return np.sin(x)
def simpson_13(f, xi, xf, num_interval):
if(num_interval%2==0):
num_interval+=1
x=np.linspace(xi, xf, num_interval)
integ=0.0
h=x[1]-x[0]
# 2씩 증가
for i in range(0, num_interval-2, 2):
integ+=(f(x[i+2])+4*f(x[i+1])+f(x[i]))*h/3
return integ
integral=simpson_13(f, 0, np.pi, 100)
print("integral:", integral)
- Simpson’s 3/8 Rule

import numpy as np
def f(x):
return np.sin(x)
def simpson_38(f, xi, xf, num_interval):
if(num_interval%3==0):
num_interval+=1
elif(num_interval%3==2):
num_interval+=2
x=np.linspace(xi, xf, num_interval)
integ=0.0
h=x[1]-x[0]
# 3씩 증가
for i in range(0, num_interval-3, 3):
integ+=(f(x[i])+3*f(x[i+1])+3*f(x[i+2])+f(x[i+3]))*3*h/8
return integ
integral=simpson_38(f, 0, np.pi, 100)
print("integral:", integral)
- Monte Carlo Integration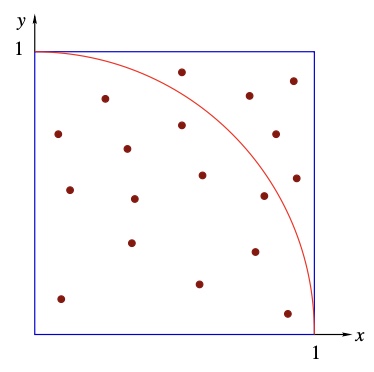 Area of the quarter circle: PI/4
Area of the quarter circle: PI/4
Find PI:
 Area of the quarter circle: PI/4
Area of the quarter circle: PI/4x, y에 대하여 0<=x<=1, 0<=y<=1 쌍을 랜덤하게 생성
y<=sqrt(1-x^2) N_circle 추가
p=N_circle/N=PI/4, then PI=4*N_circle/N
import random as rd
import numpy as np
N_tot=int(1e+4)
N_circle=0
xx=[]
yy=[]
for i in range(N_tot):
x=rd.random()
y=rd.random() # [0, 1] 값 리턴
xx.append(x); yy.append(y)
if(y<=np.sqrt(1-x**2)):
N_circle+=1
p=N_circle/N_tot
PI=p*4.
print("PI:", PI)
import matplotlib.pyplot as plt
x_circle=[]; y_circle=[]
for theta in np.linspace(0, np.pi/2, 100):
x_circle.append(np.cos(theta))
y_circle.append(np.sin(theta))
plt.plot(x_circle, y_circle)
plt.plot(xx, yy, 'ro', ms=0.2)
ax=plt.gca() # x-y 비율 조정
ax.set_aspect('equal')
plt.show()
MonteCarlo 방법은 iter=1e+8을 한번 수행하는 것 보다,
iter=1e+4을 두번 수행해서 평균낸 결과가 더 오차가 적다고 알려져 있다.
MC integral
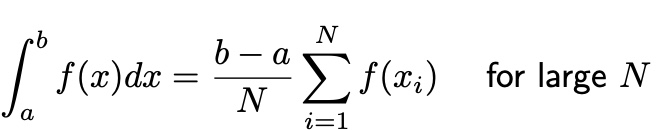
f(x_i)는 f(x)에서 랜덤하게 샘플링한 값
# integral sin(x) dx from x=0, to pi
import random as rd
import numpy as np
N=10000
rd.seed()
def f(x):
return np.sin(x)
a=0; b=np.pi
sum=0.
for i in range(N):
x=a+(b-a)*rd.random()
sum+=f(x)
sum=sum*(b-a)/N
print("SUM:", sum)
MC integral은 이전의 rectangular method, simpson method와 달리 계속 값이 변동됨
- Monte Carlo Method - Buffon’s Needle
Find PI:

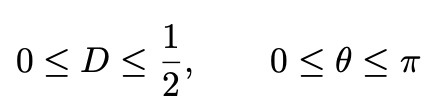 Use the probability that the needle touch or cross the lines.
Use the probability that the needle touch or cross the lines.
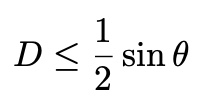
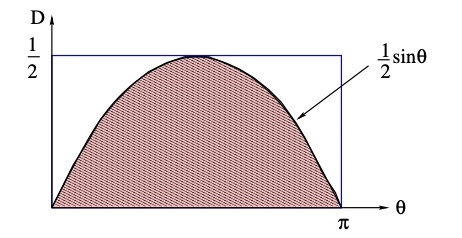


Two random variables,
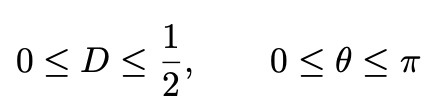 Use the probability that the needle touch or cross the lines.
Use the probability that the needle touch or cross the lines.needle touch black line when,
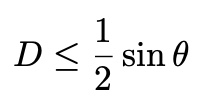
with x=theat, y=D


# Buffon's Needle
import random as rd
import numpy as np
import matplotlib.pyplot as plt
def plot_needles(n_needle):
plt.figure(figsize=(14, 7))
Lmin=0.; Lmax=3.
topline_x=[Lmin, Lmax]
topline_y=[1.0, 1.0]
bottomline_x=[Lmin, Lmax]
bottomline_y=[0, 0]
plt.plot(topline_x, topline_y, 'b', linewidth=3)
plt.plot(bottomline_x, bottomline_y, 'b', linewidth=3)
center_x=np.empty(n_needle, float)
for i in range(n_needle):
center_x[i]=rd.random()*Lmax # [0, Lmax]
# theta global 정의
x=[center_x[i]-np.cos(theta[i])*0.5, center_x[i]+np.cos(theta[i])*0.5]
y=[center_y[i]-np.sin(theta[i])*0.5, center_y[i]+np.sin(theta[i])*0.5]
plt.plot(x, y, 'r')
plt.xlim(-0.5, 3.5)
plt.ylim(-0.5, 1.5)
ax=plt.gca()
plt.show()
if __name__=="__main__":
n=[10, 100, 500, 1000]
for nn in n:
rd.seed()
theta=np.empty(nn, float)
center_y=np.empty(nn, float)
D=np.empty(nn, float)
N_count=0
for i in range(nn):
theta[i]=np.pi*rd.random()
center_y[i]=rd.random()
if center_y[i]>0.5:
D[i]=1.-center_y[i]
else:
D[i]=center_y[i]
if D[i]<=np.sin(theta[i])/2.:
N_count+=1
p=N_count/nn
print("pi=", 2.0/p)
plot_needles(nn)
MC integral은 Multidimensional Integral과 같이 복잡한 적분에서 기존의 알고리즘보다
더 빠르고 효율적으로 값을 찾을 수 있다.
Improper Integral

- range of integral: infinite
- Interand contains a singularity with in the integration range


infinite range인 경우, 적당한 수준에서 범위를 끊어 오차 타협을 봐야 함