Estimate the value between data

fitting과 달리 데이터를 함수에 맞춤

- Polynomial interpolation

Weierstrass theorem:

In general a continuous function f(x)

in a finite interval x in [a, b] can be fitted by a polynomial P(x)

Find a polynomial approximation for f(x) from N paris of numbers {(x_i, f(x_i))} for i=0, 1, … N-1

Lagrange Interpolation

with Lagrange Polynomial,

(x_k를 빼는 경우는 없음 주의)

then,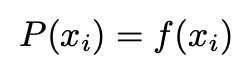

and P(x) cross every (x_i, f(x_i)) points

# Lagrange Interpolation

import numpy as np

import matplotlib.pyplot as plt

x=np.linspace(0, 2*np.pi, 11)

y=np.sin(x)

# want to find f(xxx)

xxx=np.linspace(0, 2*np.pi, 50)

# P_x is Polynomial estimate f(xxx)

P_x=[]

def p(k, xx, x): # xx 는 찾고 싶은 값, x는 주어진 점(k는 x의 인덱스)

p_k=1

for i in range(len(x)):

if i!=k:

p_k*=(xx-x[i])/(x[k]-x[i])

return p_k

for xx in xxx:

yy=0

for k in range(len(x)):

yy+=p(k, xx, x)*y[k]

P_x.append(yy)

plt.plot(xxx, P_x, 'ro')

plt.plot(x, y, 'bx')

plt.show()

단 구하고자 하는 Polynomial의 차수가 너무 크면, 정확도가 떨어짐

Cubic-Spline

3차원 보간법(부드럽게 각 점들을 이어줌)

4개의 조건을 이용해, a+bx+cx^2+dx^3의 4개의 미지수를 계산