ADALINE(ADAptive LInear NEuron)
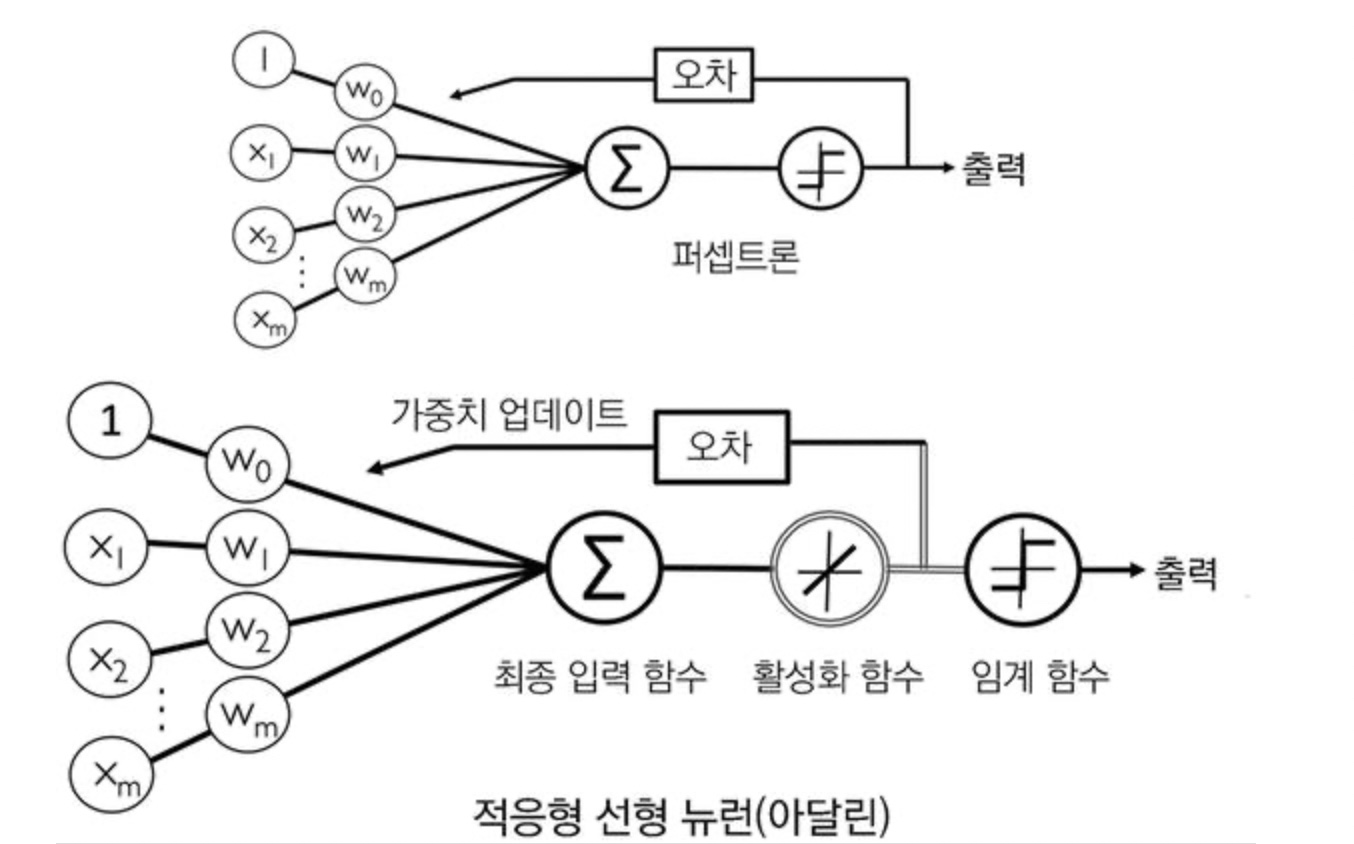
가중치를 업데이트 하는데 Percpetron의 단위 계단 함수 대신 선형 활성화 함수를 사용한다.
최종 예측을 하는데는 여전히 임계함수(단위 계단 함수)사용

경사 하강법으로 비용 함수 최소화
아달린은 계산된 출력과 진짜 클래스 레이블 사이의 제곱 오차합(Sum of Squared Errors, SSE)으로
가중치를 학습하기 위한 비용 함수 J를 정의한다.
경사하강법을 이용하여 그레이디언트 J(w)의 반대 방향으로 조금씩 가중치를 업데이트
class AdalineGD(object):
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta=eta
self.n_iter=n_iter
self.random_state=random_state
def fit(self, X,y):
rgen=np.random.RandomState(self.random_state)
self.w_=rgen.normal(loc=0.0, scale=0.01, size=1+X.shape[1])
self.cost_=[]
for _ in range(self.n_iter):
net_input=self.net_input(X)
output=self.activation(net_input)
errors=(y-output)
self.w_[1:]+=self.eta*X.T.dot(errors)
self.w_[0]+=self.eta*errors.sum()
cost=(errors**2).sum()/2.0
self.cost_.append(cost)
return self
def net_input(self,X):
return np.dot(X,self.w_[1:])+self.w_[0]
def activation(self,X):
return X
def predict(self,X):
return np.where(self.activation(self.net_input(X))>=0,1,-1)
에포크 횟수 대비 비용 함수의 값을 그래프로 나타내면 아달린 구현이 훈련 데이터에서 얼마나 잘 학습하는지 볼 수 있다.
import matplotlib.pyplot as plt
fig, ax=plt.subplots(nrows=1, ncols=2, figsize=(10,4))
ada1=AdalineGD(n_iter=10,eta=0.01).fit(X,y)
ax[0].plot(range(1,len(ada1.cost_)+1),np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline-Learning rate 0.01')
ada2=AdalineGD(n_iter=10, eta=0.0001).fit(X,y)
ax[1].plot(range(1, len(ada2.cost_)+1), ada2.cost_,marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline-Learning rate 0.0001')
plt.show()
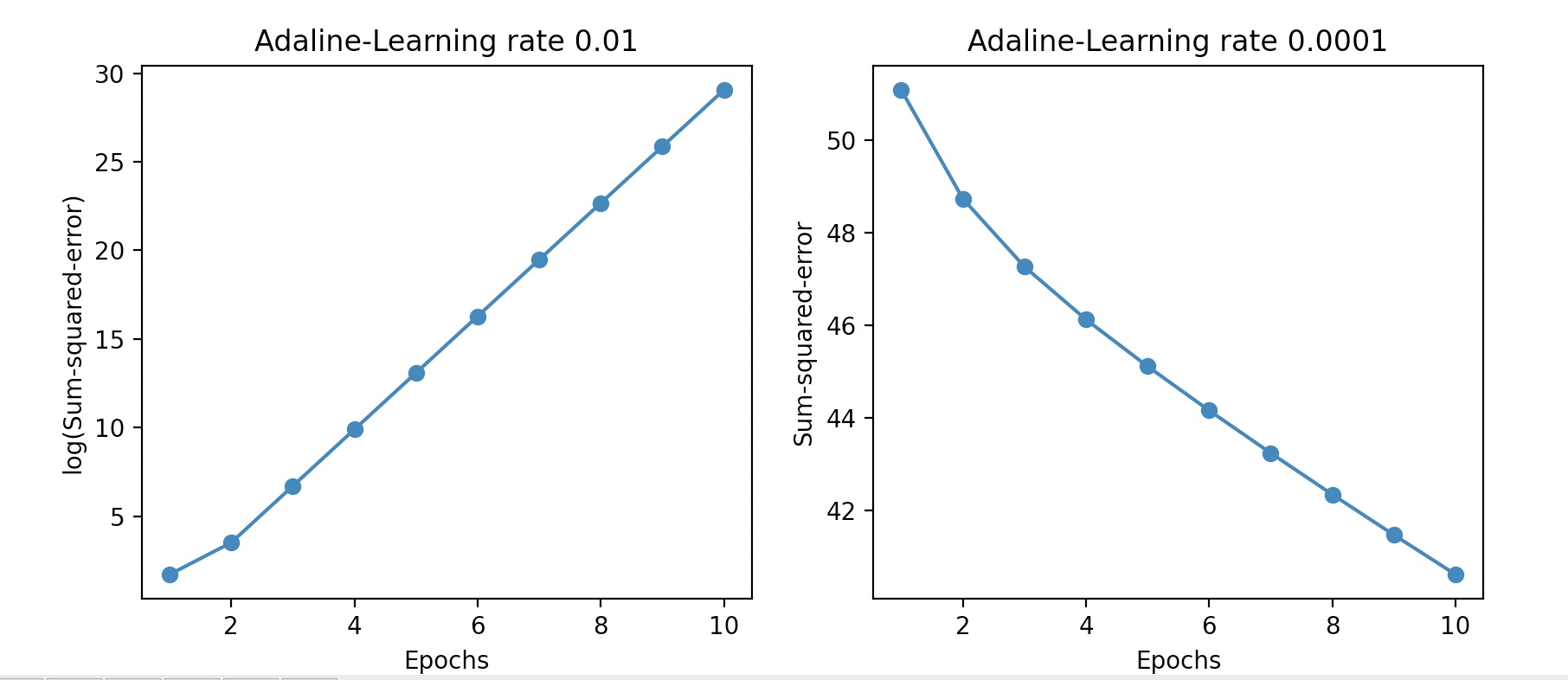
학습률이 너무 크면, 오차는 에포크 마다 점점 더 커지며,
학습률이 너무 작으면, 오차는 감소하지만 적역 최솟값에 수렴하려면 아주 많은 에포트가 필요 하다.
알고리즘들은 최적의 성능을 위해 어떤 식으로든지 특성 스케일을 조정 하는 것이 필요하다.
경사 하강법(standardization)
정규화 과정은 데이터에 평균이 0이고 단위 분산을 갖는 표준 정규 분포의 성질을 부여하여
경사 하강법 학습이 좀더 빠르게 수렴되도록 돕는다.
데이터 표준화 코드
X_std=np.copy(X)
X_std[:,0]=(X[:,0]-X[:,0].mean())/X[:,0].std()
X_std[:,1]=(X[:,1]-X[:,1].mean())/X[:,1].std()
ada=AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)
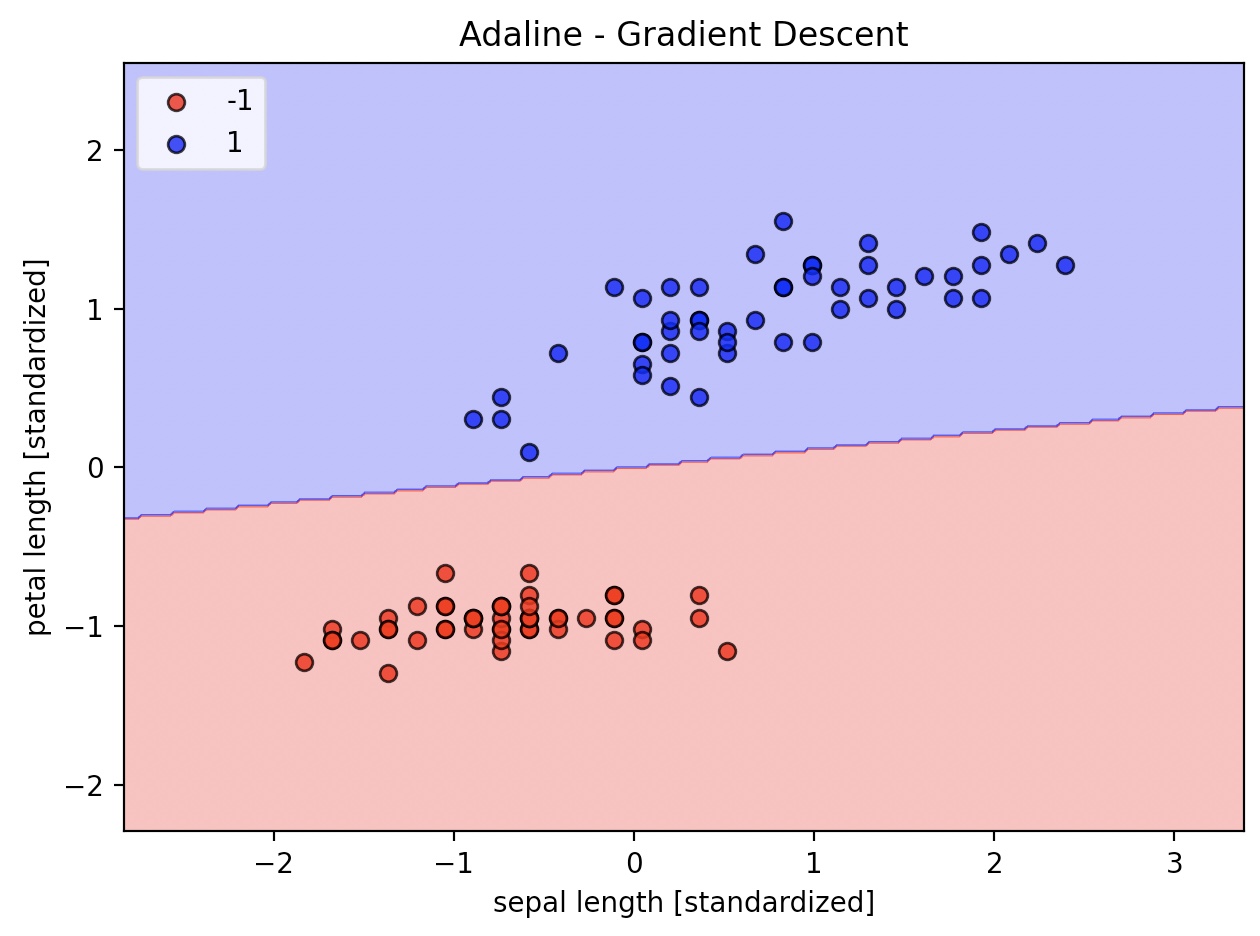
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
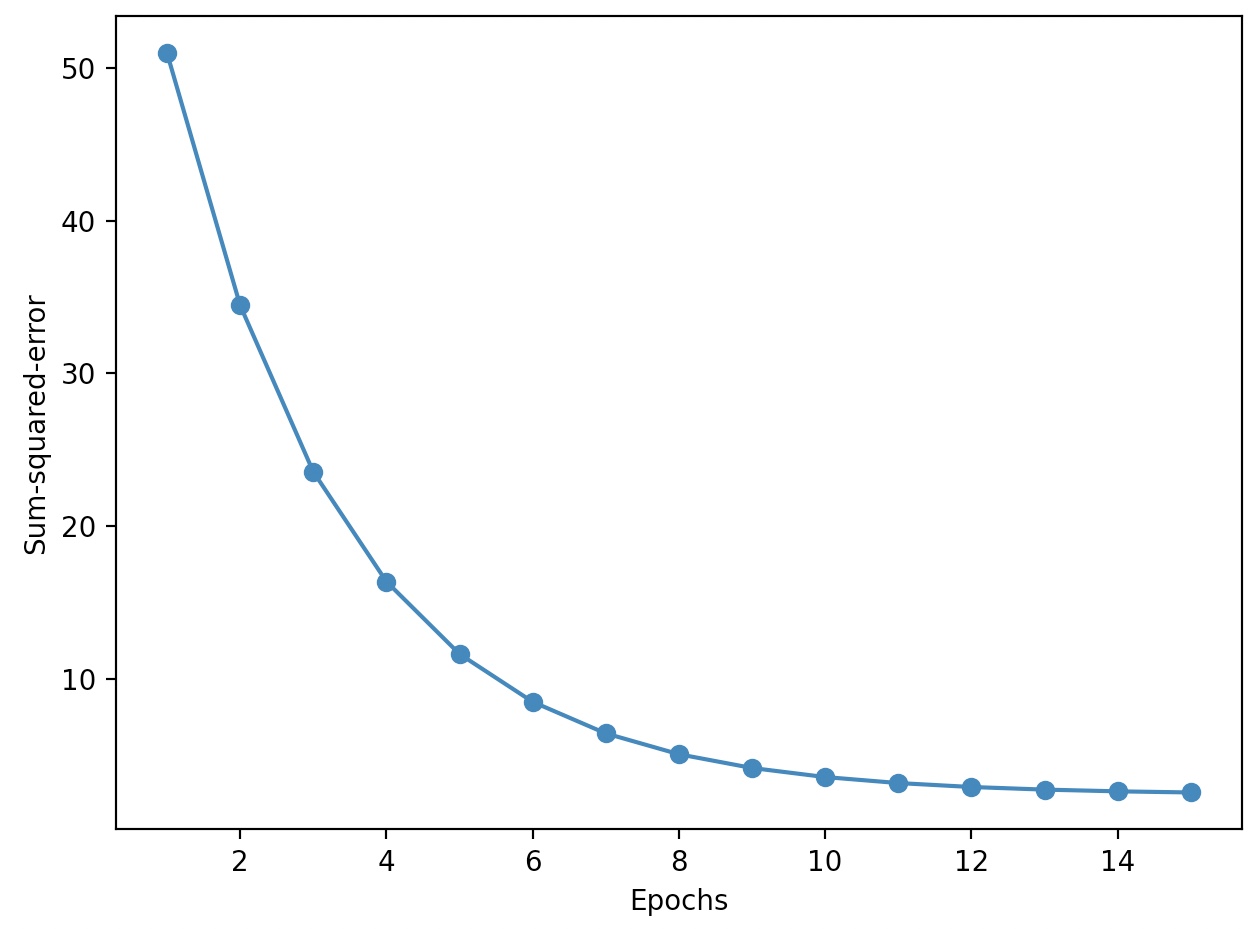
plt.plot(range(1, len(ada.cost_)+1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')
plt.tight_layout()
plt.show()