DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
DBSCAN 알고리즘은 k-means 처럼 원형 클러스터를 가정하지 않으며,
임계층을 수동으로 지정해야 하는 계층적인 방식으로 데이터셋을 나누지 않는다(hierarchical clustering)
밀집도 기반 군집 알고리즘은 샘플이 조밀하게 모인 지역에 클러스터 레이블을 할당한다.
밀집도: 특정 반경 안에 있는 샘플 개수
레이블 할당 조건
- 어떤 샘플의 특정 반경 안에 있는 이웃 샘플이 지정된 개수(MinPts) 이상이면, 핵심 샘플(core point)이 된다.
- 반경 이내에 MinPts 보다 이웃이 적지만 다른 핵심 샘플의 반경 안에 있으면 경계 샘플(border point)가 된다.
- 핵심 샘플과 경계 샘플이 아닌 모든 샘플은 잡음 샘플(noise point)가 된다.

Process of DBSCAN
1. 개별 핵심 샘플이나 핵심 샘플의 그룹(반경 이내에 있는 핵심 샘플을 연결)을 클러스터로 만든다.
2. 경계 샘플을 해당 핵심 샘플의 클러스터에 할당한다.
DBSCAN은 클러스터를 모양을 원형으로 가정하지 않으며,
k-means나 Hierarchical clustering과 달리 샘플을 클러스터에 할당하지 않고 잡음 샘플을 구분하는 능력이 있다.
(잡음 샘플에 -1 레이블을 할당)
반달 모양 예제 데이터셋
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
X, y=make_moons(n_samples=200, noise=0.05, random_state=0)
plt.scatter(X[:, 0], X[:, 1])
plt.tight_layout()
plt.show()

k-means와 complete linkage Hierarchical clustering을 이용한 반달 모양 데이터셋 분류
from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering
f, (ax1, ax2)=plt.subplots(1, 2, figsize=(8, 3))
km=KMeans(n_clusters=2, random_state=0)
y_km=km.fit_predict(X)
ax1.scatter(X[y_km==0, 0], X[y_km==0, 1], c='lightblue', edgecolor='black', marker='o', s=40, label='cluster 1')
ax1.scatter(X[y_km==1, 0], X[y_km==1, 1], c='red', edgecolor='black', marker='s', s=40, label='cluster 2')
ax1.set_title('K-means clustering')
ac=AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='complete')
y_ac=ac.fit_predict(X)
ax2.scatter(X[y_ac==0, 0], X[y_ac==0, 1], c='lightblue', edgecolor='black', marker='o', s=40, label='Cluster 1')
ax2.scatter(X[y_ac==1, 0], X[y_ac==1, 1], c='red', edgecolor='black', marker='s', s=40, label='Cluster 2')
ax2.set_title('Agglomerative clustering')
plt.legend()
plt.tight_layout()
plt.show()
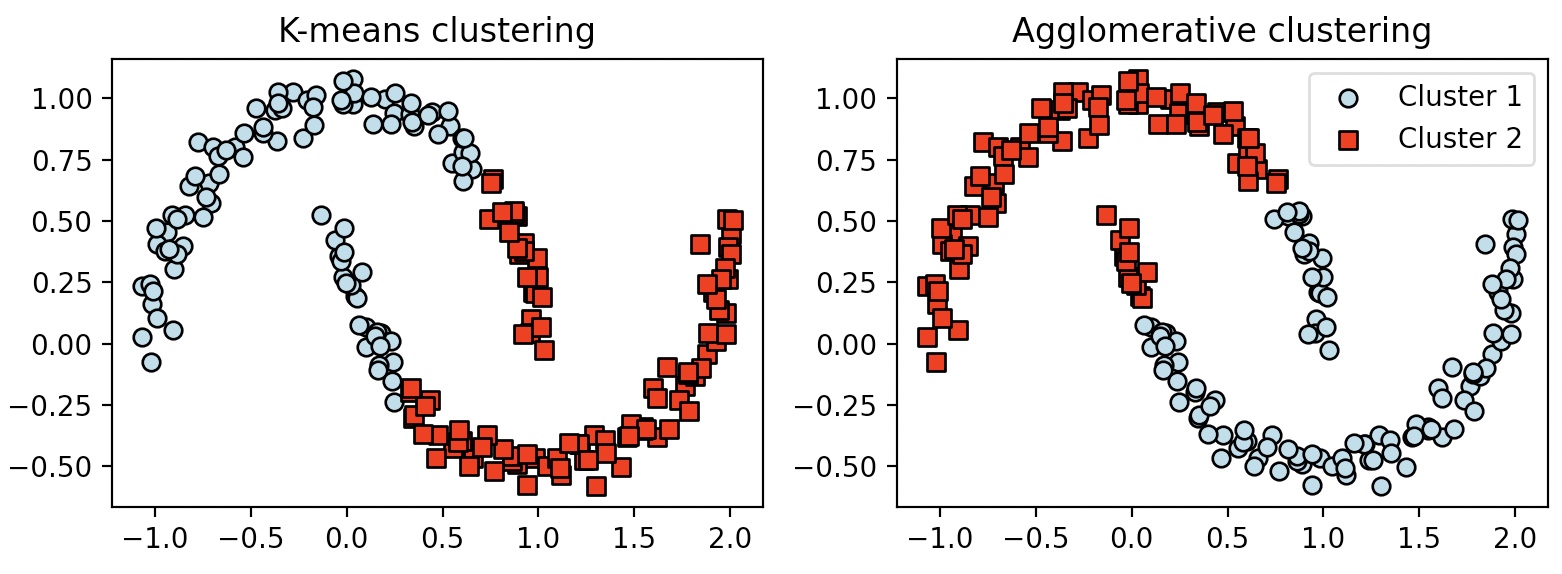
두 알고리즘 모두 복잡한 형태를 잘 처리하지 못한다.
from sklearn.cluster import DBSCAN
db=DBSCAN(eps=0.2, min_samples=5, metric='euclidean')
y_db=db.fit_predict(X)
plt.scatter(X[y_db==0, 0], X[y_db==0, 1], c='lightblue', edgecolor='black', marker='o', s=40, label='Cluster 1')
plt.scatter(X[y_db==1, 0], X[y_db==1, 1], c='red', edgecolor='black', marker='s', s=40, label='Cluster 2')
plt.legend()
plt.tight_layout()
plt.show()
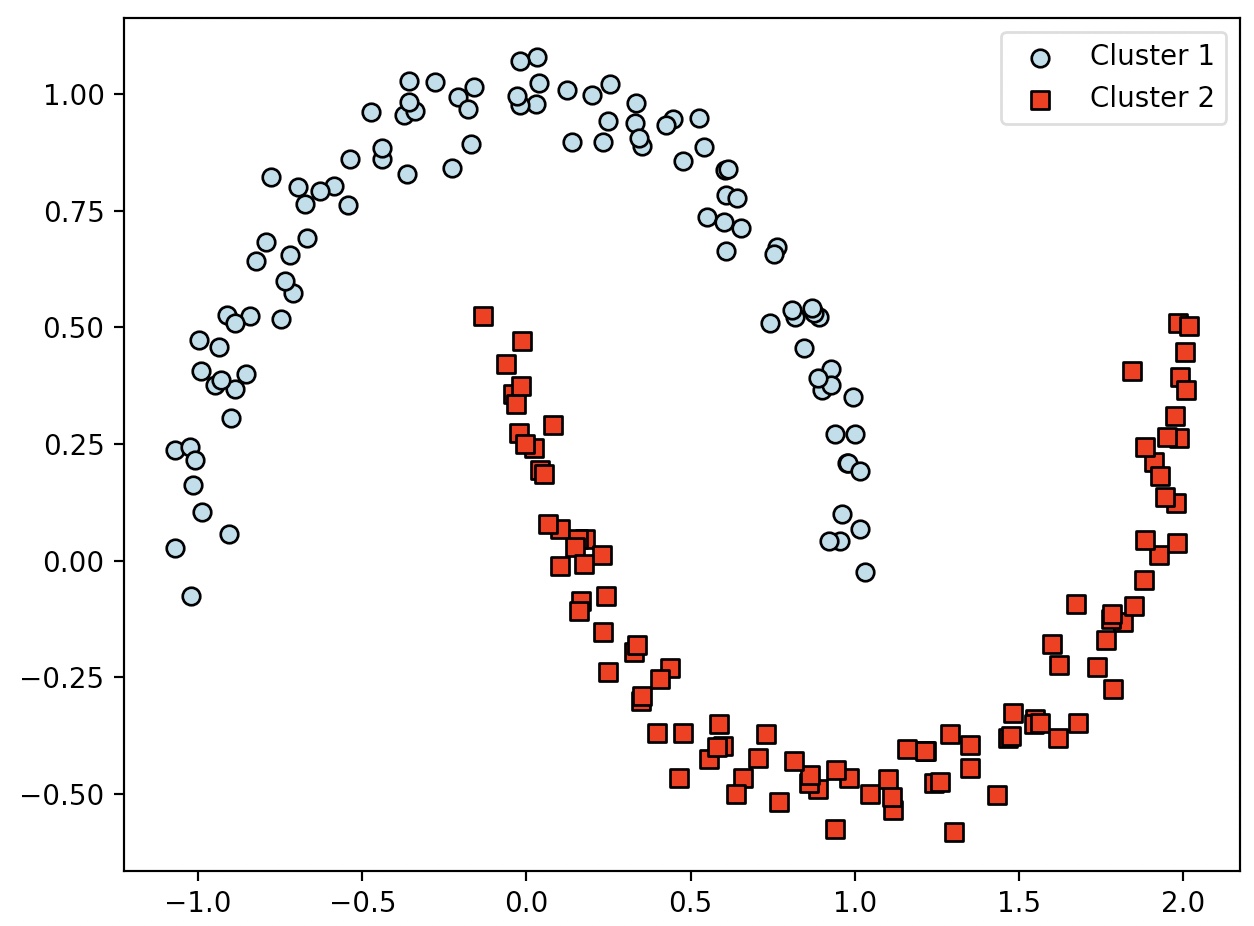
DBSCAN 알고리즘은 성공적으로 복잡한 데이터셋을 처리한다
DBSCAN은 임의 형태의 데이터를 처리할 수 있는 능력이 뛰어나다.
하지만 DBSCAN은 데이터셋에서 훈련 샘플 개수가 고정되어 있다고 가정하고 특성 개수가 늘어나면 차원의 저주로 인한 역효과가 증가한다.
차원의 저주는 유클리디안 거리 측정을 사용하는 다른 군집 알고리즘에도 영향을 미친다.
(k-means, KDBSCAN …)
DBSCAN이 좋은 군집 결과를 만들기 위해서는 하이퍼 파라미터(MinPts와 반경 크기)를 최적화 해야 한다.
차원 축소 기법을 적용해서 차원의 저주 문제를 줄일 수 있다.(주성분 분석, RBF 커널 주성분 분석-비지도 학습)
병합 군집과 DBSCAN은 알고리즘 특징상 새로운 데이터 예측을 할 수 없다.
AgglomerativeClustering, DBSCAN에는 fit_predict 메서드만 있다.(fit_transform은 없다.)
데이터세을 2차원 부분 공간으로 압축하면 2차원 산점도에서 클러스터를 시각화하고 레이블을 할당할 수 있다.