긴 시퀀스 학습의 어려움
BPTT(BackPropagatio)는 손실 함수의 그레이디언트를 계산할 때, 곱셈항 dh_t/dh_k 때문에
그레이디언트 폭주(exploding gradient) 혹은 그레이디언트 소실(vanishing gradient)문제가 발생한다.
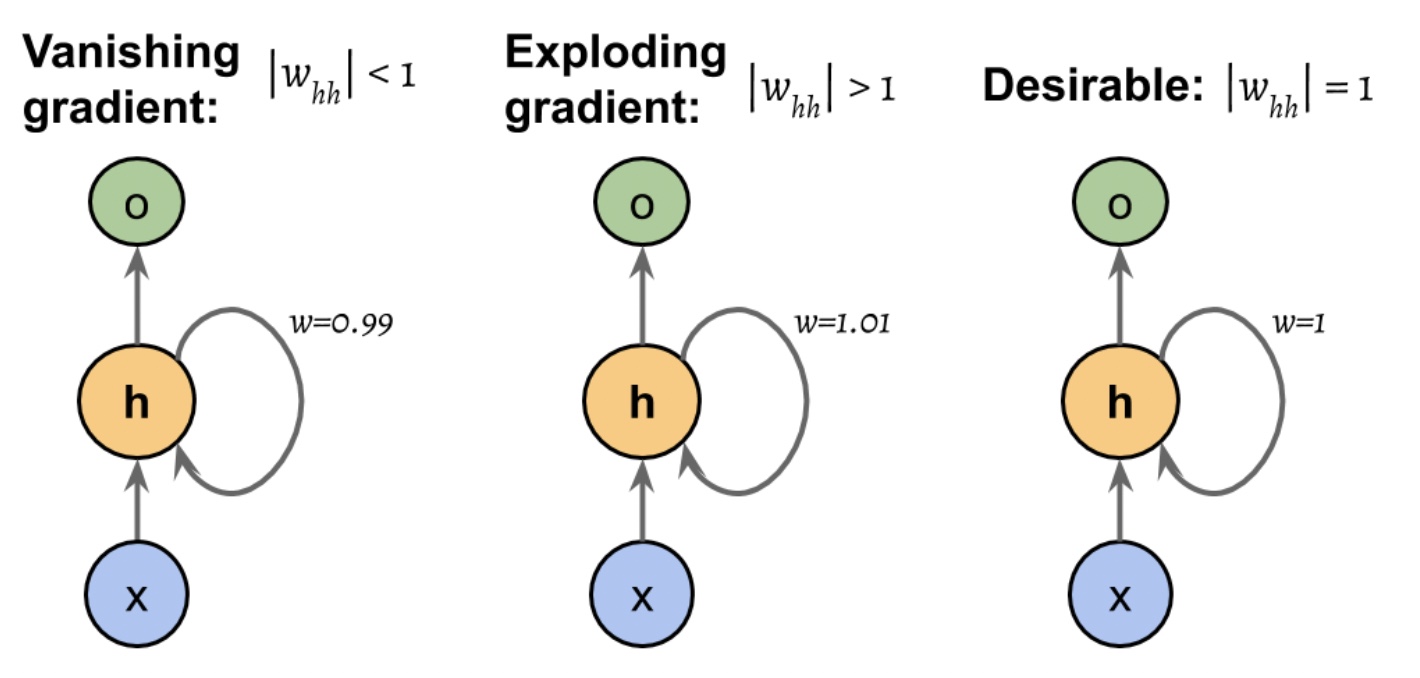
dh_t/dh_k는 t-k개의 곱셈으로 이루어져 있다.(chain rule)
가중치 w가 t-k번 곱해져 w^(t-k)가 된다.
abs(w)<1이면, t-k가 클 때 매우 작아지게 되고,
abs(w)>1이면, t-k가 커질 때 w^(t-k)가 매우 커진다.
(t-k가 크다는 것은 긴 시간 의존성을 가진다는 것을 의미한다.)
그레이디언트 소실이나 폭주를 피하기 위해서는 abs(w)=1이 되도록 만들어야 한다.
그레이디언트 폭주와 소실 해결책
- 그레이디언트 클리핑
- TBPTT(Truncated BackPropagation Through Time)
- LSTM(Long Short-Term Memory)
그레이디언트 클리핑
그레이디언트 임계값을 지정하고 이 값을 넘어서는 경우 임계 값을 그레이디언트 값으로 사용한다.
TBPTT(Truncated BackPropagation Through Time)
정방향 계산 후 역전파될 수 있는 타임 스텝의 횟수를 제한한다.
ex) 시퀀스가 100개의 원소 또는 스텝을 가지더라도, 가장 최근 20번의 타임 스텝만 역전파
LSTM(Long Short Term Memory)
LSTM은 그레이언트 소실 문제를 극복하기 위해 소개되었으며, LSTM의 기본 구성 요소는
일반 RNN의 은닉층을 대체하는 메모리 셀이다.

LSTM에서 셀 상태(C)와 은닉 상태(h)가 다음 타음 스탭으로 순환된다.
이전 타임 스텝의 셀 상태 C_t-1은 어떤 가중치와도 직접 곱해지지 않고 변경되어 현재 타임 스텝의 셀 상태 C_t를 얻는다.
x_t는 타임 스텝 t에서 입력 데이터이고, h_t-1은 타임 스텝 t-1에서 은닉 유닛의 출력이다.
sigma는 시그모이드 함수를 tanh는 하이퍼 탄젠트 활성화 함수로 네 개의 상자는 일련의 가중치로 표시된다.
입력 h_t-1, x_t에 대하여 행렬-벡터 곱셈을 수행한 후 선형 조합된다.
시그모이드 함수로 계산하는 유닛을 게이트라고 한다.
LSTM에는 삭제 게이트(forget gate), 입력 게이트(input gate), 출력 게이트(output gate)가 존재한다.
삭제 게이트(forget gate)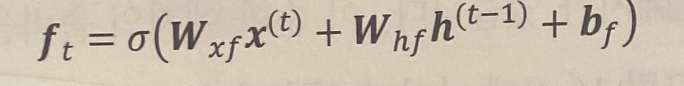
메모리 셀이 무한정 성장하지 않도록 셀 상태를 다시 설정한다.
삭제 게이트가 통과할 정보와 억제할 정보를 결정한다.
입력 게이트 & 후보값(C~)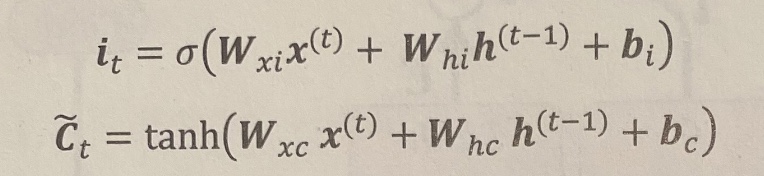

셀 상태를 업데이트하는 역할을 담당한다.
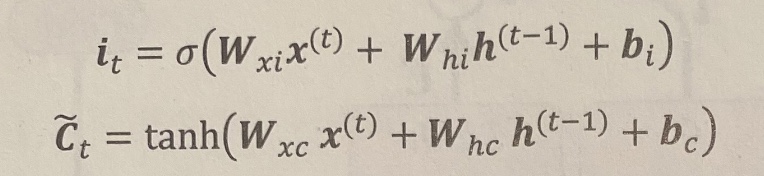
입력 게이트와 후보값을 이용해서 아래와 같이 셀 상태를 계산한다.

출력 게이트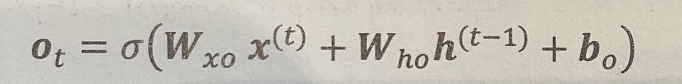

은닉 유닛의 출력 값을 업데이트한다.
위의 모든 계산값을 이용해서 현재 타임 스텝에서 은닉 유닛의 출력을 아래와 같이 계산한다.

LSTM은 의존성이 긴 시퀀스를 모델링하는 기본적인 방법을 제공한다.
GRU는 LSTM보다 구조가 단순하기 때문에 계산 효율성이 높다.
폴리포닉(polyphonic) 음악 모델링 같은 일부 작업의 성능을 LSTM과 견줄만 하다.