Overfitting
모델 파라미터가 훈련 데이터셋에 있는 특정 샘플들에 대해 너무 가깝게 맞추어져 있다는 뜻이다.
(새로운 데이터에 잘 일반화하지 못하기 때문에 분산이 크다고 말한다.
과대적합의 이유는 주어진 훈련 데이터에 비해 모델이 너무 복잡하기 때문이다.
일반화 오차를 감소시키기 위해 많이 사용하는 방법
- 더 많은 훈련 데이터를 모은다.
- 규제를 통해 복잡도를 제한한다.
- 파라미터 개수가 적은 간단한 모델을 사용한다.
- 데이터 차원을 줄인다.


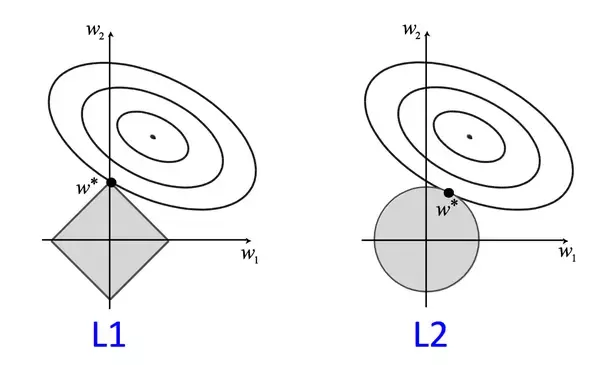
L1규제(좌측)과 L2규제(우측); L1 regularization, L2 regularization
L2규제에서 가중치 제곱을 가중치 절댓값으로 바꾸면 L1규제가 된다.
L1규제는 L2규제와 대조적으로 보통 희소한 특성 벡터를 만든다. 대부분의 특성 가중치가 0이 된다.
실제로 관련 없는 특성 데이터가 많은 고차원 데이터셋의 경우 이런 희소성이 도움이 된다.(훈련샘플보다 관련 없는 특성이 많은 경우)
L2 규제의 기하학적 해석
L2 규제는 비용 함수에 패널티 항(penalty term)을 추가한다. 이는 규제가 없는 비용 함수로 훈련한 모델에 비해
가중치 값을 매우 작게 만드는 효과가 있다.
(비용함수에 추가하는 패널티 항을 규제로 볼 수 있다.-> 큰 가중치를 제한함)
규제 파라미터 lambda로 규제의 강도를 크게 하면 가중치가 0에 가까워 지고 훈련 데이터에 대한 모델 의존성은 줄어든다.
규제 파라미터가 커질수록 패널티 비용이 빠르게 증가하여 L2 공을 작게 만든다.
규제가 없는 비용과 패널티 항의 합을 최소화해야 한다.
이는 학습할 만한 충분한 훈련 데이터가 없을 때 편향을 추가하여 모델을 간단하게 만듦으로써 분산을 줄이는 것으로 해석 가능하다.
L1 규제를 사용한 희소성
L1 규제의 등고선은 날카롭기 때문에 비용 함수의 포물선과 L1 다이아몬드의 경계가 만나는 최적점은 축에 가깝게 위치할 가능성이 높다.
이는 희소성이 나타나는 이유이다.
Scikit-learn의 L1규제를 통한 희소한 모델
from sklearn.linear_model import LogisticRegression
LogisticRegression(solver='liblinear', penalty='l1')
‘lbfgs’는 L1 규제를 지원하지 않음(위의 소스코드는 대신 ‘liblinear’를 사용)
lr=LogisticRegression(solver='liblinear', penalty='l1', C=1.0, random_state=1)
#규제효과를 높이거나 낮추려면 C값을 증가시키거나 감소시킨다.
lr.fit(X_train_std, y_train)
print("훈련 정확도:", lr.score(X_train_std, y_train))
print("테스트 정확도:", lr.score(X_test_std, y_test))
훈련 정확도: 1.0
테스트 정확도: 1.0
lr.intercept_ 를 통해서 절편을 확인해 보면 세개의 값이 들어 있는 배열이 반환된다.
lr.intercept_
array([-1.26392152, -1.21596534, -2.37040177])
위의 절편은 OvR(One-Versus-Rest) 방식을 사용하기 때문에
첫 번째 절편은 클래스1을 클래스2, 3을 구분하는 모델이고,
두 번째 절편은 클래스2을 클래스1, 3과 구분하는 모델이고,
세 번째 절편은 클래스3을 클래스1, 2과 구분하는 모델이다.
lr.coef_ 속성에 있는 가중치는 클래스마다 벡터 하나씩 세 개의 행이 있는 가중치 배열이다.
(각 행은 13개의 가중치를 가진다.)
각 가중치와 13차원의 wine데이터셋의 특성을 곱해 최종 입력을 계산한다.
lr.coef_
array([[ 1.24567209, 0.18072301, 0.74682115, -1.16438451, 0. ,
0. , 1.1595535 , 0. , 0. , 0. ,
0. , 0.55864751, 2.50891241],
[-1.53644846, -0.38769843, -0.99485417, 0.36489012, -0.05989298,
0. , 0.66853184, 0. , 0. , -1.93460212,
1.23246414, 0. , -2.23212696],
[ 0.1355558 , 0.16880291, 0.35718019, 0. , 0. ,
0. , -2.43768478, 0. , 0. , 1.5635432 ,
-0.81834553, -0.4930494 , 0. ]])
intercept_는 w0에 해당하며,
coef_에 있는 값은 j>0인 wj이다.
이와 같이 L1 규제는 결과적으로 데이터셋에 관련된 적은 특성이 있더라도 견고한 모델을 만들어 준다.
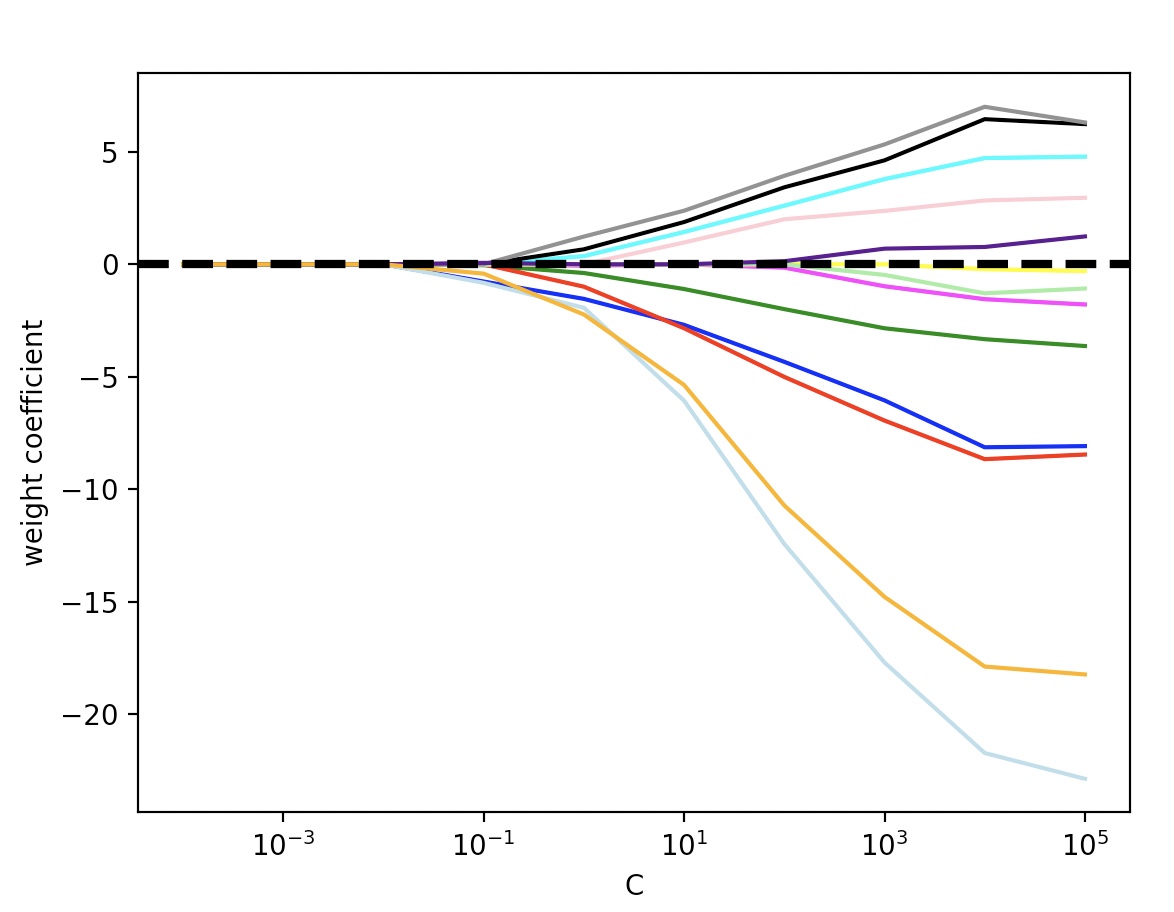
규제강도를 높여(C의 값을 낮춤) 희소성을 더 강하게 할 수 있다.->0인 원소가 더 많아짐
규제 강도에 따른 특성의 가중치 변화
import matplotlib.pyplot as plt
fig=plt.figure()
ax=plt.subplot(111)
colors=['blue', 'green', 'red', 'cyan', 'magenta' ,'yellow', 'black', 'pink' ,'lightgreen' ,'lightblue', 'gray' ,'indigo' ,'orange']
weights, params=[], []
for c in np.arange(-4., 6.):
lr=LogisticRegression(solver='liblinear', penalty='l1', C=10.**c, random_state=0)
lr.fit(X_train_std,y_train)
weights.append(lr.coef_[1])
params.append(10**c)
weights=np.array(weights)
for column, color in zip(range(weights.shape[1]), colors):
plt.plot(params, weights[:, column], label=df_wine.columns[column+1], color=color)
plt.axhline(0, color='black', linestyle='--', linewidth=3)
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.xscale('log')
plt.legend(loc='upper left')
ax.legend(loc='upper center', bbox_to_anchor=(1.38, 1.03), ncol=1, fancybox=True)
plt.show()